b) DIBUJO ASISTIDO POR COMPUTADORA (BIO)
Para integrarla se ha hecho un análisis de la importancia de estos conocimientos, identificando los temas más relevantes y que tienen una mayor aplicación en el quehacer profesional.
Puesto que esta materia dará soporte a otras, más directamente vinculadas con desempeños profesionales; se inserta al inicio de la trayectoria escolar; antes de cursar aquéllas a las que da soporte.
De manera general lo estudiado y elaborado en esta asignatura se aplica en el estudio de los temas:
Normas para la elaboración e interpretación de dibujos, herramientas básicas del software de dibujo, edición de dibujos, perspectivas, acotación, dibujo de sólidos, ensambles y de conjunto, entre otros.

c) DIBUJO INDUSTRIAL
Así como obtiene la capacidad de dibujar en un software que le permita tener mayor facilidad de adquirir un empleo ya que hoy en día todos los diseños de los productos, escantillones, lay-out y herramentales; son realizados por medio de software. Por otro lado, el simple hecho de dominar esta herramienta le abre la puerta no solo en el área de la ingeniería industrial sino también en el área de
dibujo mecánico, dibujo civil.
Esta materia se convierte en una competencia previa para las asignaturas de Metrología debido a que debe dibujar piezas para luego medirlas, Estudio del Trabajo I, ya que se dibujan herramentales de diferentes procesos, entre otras.
CALCULO DIFERENCIAL
Plantea y resuelve problemas utilizando las definiciones de límite y derivada de funciones de una variable para la elaboración de modelos matemáticos aplicados

CALCULO DIFERENCIAL
CALCULO DIFERENCIAL

Cálculo Diferencial
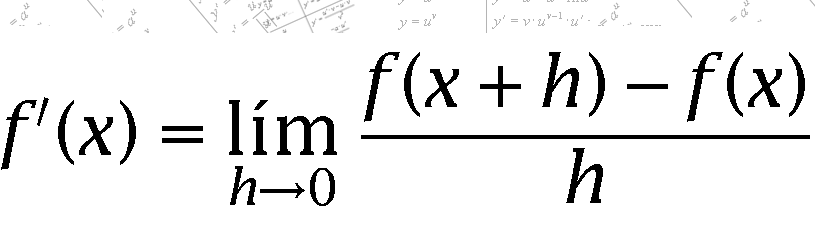
CLCULO DIFERENCIAL
La importancia del estudio del Cálculo Diferencial radica principalmente en proporcionar las bases para los temas en el desarrollo de las competencias del Cálculo Integral, Cálculo Vectorial, Ecuaciones Diferenciales y asignaturas de física y ciencias de la ingeniería, por lo que se pueden diseñar proyectos integradores con cualquiera de ellas.
La característica más sobresaliente de esta asignatura es que en ella se estudian las bases sobre las que se construye el cálculo diferencial. Utilizando las definiciones de función y límite se establece uno de los conceptos más importantes del cálculo: la derivada, que permite analizar razones de cambio y problemas de optimización, entre otras. La derivada es tema de trascendental importancia en las aplicaciones de la ingeniería.
Competencias Previas:
Utiliza la aritmética para realizar operaciones.
Emplea el álgebra para simplificar expresiones.
Resuelve ecuaciones y sistemas de ecuaciones.
Utiliza la trigonometría para resolver problemas.
Describe las ecuaciones de los principales lugares geométricos.
Competencias a Desarrollar:
Plantea y resuelve problemas utilizando las definiciones de límite y derivada de funciones de una variable para la elaboración de modelos matemáticos aplicados.
Intención Didáctica:
La asignatura de Cálculo Diferencial se organiza en cinco temas.
El primer tema se inicia con un estudio sobre los números reales y sus propiedades básicas, así como la solución de problemas con desigualdades. Esto servirá de sustento para el estudio de las funciones de variable real.
El tema dos incluye el estudio del dominio y rango de funciones, así como las operaciones relativas a éstas. También las funciones simétricas, par e impar, escalonadas (definidas por más de una regla de correspondencia), crecientes y decrecientes, periódicas, de valor absoluto, etc.
En el tema tres se introduce la noción intuitiva de límite, así como la definición formal. Se aborda el cálculo de límites por valuación, factorización, racionalización, de límites trigonométricos y los límites laterales. Se incluyen casos especiales de límites infinitos y límites al infinito, así como asíntotas horizontales y verticales. El tema concluye con el estudio de la continuidad en un punto y en un intervalo.
La derivada, en el tema cuatro, se aborda de manera intuitiva obteniendo la pendiente de la recta tangente a una curva y como una razón de cambio. La definición de derivada permite deducir propiedades y reglas de derivación de funciones.
El último tema consiste principalmente en aplicar las propiedades y reglas de derivación para modelar y resolver problemas de razones de cambio y optimización específicos de cada área.
El estudiante debe desarrollar la habilidad para modelar situaciones cotidianas en su entorno. Es importante que el estudiante valore las actividades que realiza, que desarrolle hábitos de estudio y de trabajo para que adquiera características tales como: la curiosidad, la puntualidad, el entusiasmo, el interés, la tenacidad, la flexibilidad y la autonomía.
El Cálculo Diferencial contribuye principalmente para el desarrollo de las siguientes competencias genéricas: de capacidad de abstracción, análisis y síntesis, capacidad para identificar, plantear y resolver problemas, habilidad para trabajar en forma autónoma, habilidades en el uso de las TIC’s, capacidad crítica y autocrítica y la capacidad de trabajo en equipo.

Clculo Diferencial
La característica más sobresaliente de esta asignatura es que en ella se estudian los conceptos sobre los que se construye todo el Cálculo: números reales, variable, función y límite.
Utilizando estos tres conceptos se establece uno de los esenciales del Cálculo: la derivada, concepto que permite analizar razones de cambio entre dos variables, noción de trascendental importancia en las aplicaciones de la ingeniería.
Esta asignatura contiene los conceptos básicos y esenciales para cualquier área de la ingeniería y contribuye a desarrollar en el ingeniero un pensamiento lógico, formal, heurístico y algorítmico.
En el Cálculo diferencial el estudiante adquiere los conocimientos necesarios para
afrontar con éxito cálculo integral, cálculo vectorial, ecuaciones diferenciales,
asignaturas de física y ciencias de la ingeniería. Además, encuentra, también, los principios y las bases para el modelado matemático.

Calculo Diferencial 1H
Nuestro primer problema es muy antiguo; se remonta a la época del gran científico
griego Arquímedes (287-212 A. C.). Nos referimos al problema de la pendiente de la recta
tangente. Nuestro segundo problema es más reciente. Surgió con los intentos de Kepler
(1571-1630), Galileo (1564-1642), Newton (1642-1727) y otros para describir la velocidad de un cuerpo en movimiento. Es el problema de la velocidad instantánea.
Los dos problemas, uno geométrico y el otro mecánico, parecen no estar muy relacionados. En este caso, las apariencias engañan. Los dos problemas son gemelos idénticos.
La recta tangente La noción de Euclides de una tangente, como una recta que toca a una curva en un solo punto es totalmente correcta para circunferencias (véase la
figura 1); pero completamente insatisfactoria para otras curvas (véase la figura 2). La
idea de una tangente, en P a una curva como la recta que mejor se aproxima a la curva
cerca de P es bastante mejor, pero aún muy vaga para la precisión matemática. El concepto de límite proporciona una manera de obtener una mejor descripción.
Sea P un punto en una curva y sea Q un punto móvil cercano a P en esa curva.
Considere la recta que pasa por P y Q, llamada recta secante. La recta tangente en P es
la posición límite (si ésta existe) de la recta secante cuando Q se mueve hacia P a lo largo de la curva (véase la figura 3).
Suponga que la curva es la gráfica de la ecuación Entonces, P tiene
coordenadas un punto cercano Q tiene coordenadas y la
recta secante de P y Q tiene pendiente dada por (véase la figura 4):
msec = f1c + h2 - f1c2
h
msec
(c, f(c)), 1c + h, f1c + h22,
y = f1x2.
Mediante el concepto de límite, que estudiamos en el capítulo anterior, ahora podemos
dar una definición formal de la recta tangente.
P
Recta tangente en P
Figura 1
Recta tangente en P
P
Figura 2
Recta tangente
mtan msec