Ciencias Básicas

Esta asignatura contribuye a desarrollar un pensamiento lógico, heurístico y
algorítmico al modelar fenómenos y resolver problemas en los que interviene la
variación.
Hay una diversidad de problemas en la ingeniería que son modelados y resueltos a
través de una integral, por lo que resulta importante que el ingeniero domine el
Cálculo integral.
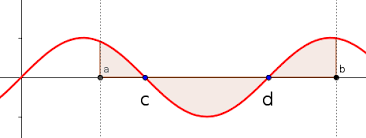
El problema esencial del Cálculo integral es calcular áreas de superficies,
particularmente el área bajo la gráfica de una función; de manera más sencilla,
sumar áreas de rectángulos. Varios conceptos son descritos como el producto de
dos variables; por ejemplo: trabajo, como fuerza por distancia; fuerza como el
producto de la presión por el área; masa como densidad por volumen. Si cada uno
de los factores que componen el producto se asocian con cada uno de los ejes
coordenados; el producto se asocia en el plano con una área que puede ser
calculada a través de una integral.
En general, si se define un plano p q, entonces la integral nos permite calcular
áreas en este plano, las unidades del área resultante están definidas por las
unidades de los factores.

Este es un curso de prueba

2. Integral indefinida y métodos de integración.

2.1Definición de integral indefinida. 2.2 Propiedades de integrales indefinidas. 2.3 Cálculo de integrales indefinidas . 2.3.1 Directas.
2.3.2 Con cambio de variable. 2.3.3 Por partes. 2.3.4 Trigonométricas. 2.3.5 Por sustitución trigonométrica. 2.3.6 Por fracciones parciales

Aquí se describen en que consisten las condiciones del curso 

La asignatura contribuye a desarrollar un pensamiento lógico-matemático al perfil del ingeniero y aporta las herramientas básicas para desarrollar el estudio del cálculo integral y sus aplicaciones. Además, proporciona herramientas que permiten modelar fenómenos de contexto. Cálculo Integral requiere como competencia previa todos los temas de Cálculo Diferencial y a su vez proporciona las bases para el desarrollo de las competencias del Cálculo Vectorial y Ecuaciones Diferenciales y asignaturas de física y ciencias de la ingeniería, por lo que se pueden diseñar proyectos integradores con cualquiera de ellas. La característica más sobresaliente de esta asignatura es que en ella se estudian las bases sobre las que se construye el cálculo integral. Utilizando las definiciones de suma de Riemann, integral definida para el cálculo de áreas. Para integral indefinida se consideran los métodos de integración como parte fundamental del curso. La integral es tema de trascendental importancia en las aplicaciones de la ingeniería.

Esta asignatura se organiza en 4 unidades o temas

En el primer tema se inicia con el concepto del cálculo de áreas mediante sumas de Riemann como una aproximación a ella. Se incluye la notación sumatoria para que el alumno la maneje. La función primitiva (antiderivada) se define junto con el Teorema de Valor Intermedio y el primer y segundo Teorema Fundamental del Cálculo. Se estudia la integral definida antes de la indefinida puesto que aquélla puede ser abordada a partir del acto concreto de medir áreas. En el segundo tema se estudia la integral indefinida y los métodos de integración principales. Se remarca la importancia de este tema para desarrollar con detalle cada uno de los métodos y considerar esto para la evaluación. El tercer tema de aplicaciones de la integral se trata del cálculo de áreas, volúmenes y longitud de arco. Otras aplicaciones de utilidad que se pueden abordar son los centroides, áreas de superficie, trabajo, etc. En el cálculo de áreas se considerarán además aquellas que requieren el uso de integrales impropias de ambos tipos. Todo lo anterior aplicado en el contexto de las ingenierías.

En el último tema de series se inicia con el concepto de sucesiones y series para analizar la convergencia de algunas series que se utilizan para resolver ciertas integrales. La serie de Taylor permite derivar e integrar una función como una serie de potencias. El estudiante debe desarrollar la habilidad para modelar situaciones cotidianas en su entorno. Es importante que el estudiante valore las actividades que realiza, que desarrolle hábitos de estudio y de trabajo para que adquiera características tales como: la curiosidad, la puntualidad, el entusiasmo, el interés, la tenacidad, la flexibilidad y la autonomía. El Cálculo Integral contribuye principalmente para el desarrollo de las siguientes competencias genéricas: de capacidad de abstracción, análisis y síntesis, capacidad para identificar, plantear y resolver problemas, habilidad para trabajar en forma autónoma, habilidades en el uso de las TIC’s, capacidad crítica y autocrítica y la capacidad de trabajo en equipo.

La asignatura contribuye a desarrollar un pensamiento lógico-matemático al perfil del ingeniero y aporta las herramientas básicas para desarrollar el estudio del calculo integral y sus aplicaciones. Además, proporciona herramientas que permiten modelar fenómenos de contexto.
Cálculo Integral requiere como competencia previa todos los temas de Cálculo Diferencial y a su vez proporciona las bases para el desarrollo de las competencias del Cálculo Vectorial y Ecuaciones Diferenciales y asignaturas de física y ciencias de la ingeniería, por lo que se pueden diseñar proyectos integradores con cualquiera de ellas.
La característica más sobresaliente de esta asignatura es que en ella se estudian las bases sobre las que se construye el cálculo integral. Utilizando las definiciones de suma de Riemann, integral definida para el cálculo de áreas. Para integral indefinida se consideran los métodos de integración como parte fundamental del curso. La integral es tema de trascendental importancia en las aplicaciones de la ingeniería.

La asignatura contribuye a desarrollar un pensamiento lógico-matemático al perfil del ingeniero y aporta las herramientas básicas para desarrollar el estudio del cálculo integral y sus aplicaciones. Además, proporciona herramientas que permiten modelar fenómenos de contexto.
La característica más sobresaliente de esta asignatura es que en ella se estudian las bases sobre las que se construye el cálculo integral. Utilizando las definiciones de suma de Riemann, integral definida para el cálculo de áreas. Para integral indefinida se consideran los métodos de integración como parte fundamental del curso. La integral es tema de trascendental importancia en las aplicaciones de la ingeniería.

La asignatura contribuye a desarrollar un pensamiento lógico-matemático al perfil del
ingeniero y aporta las herramientas básicas para desarrollar el estudio del cálculo integral y
sus aplicaciones. Además, proporciona herramientas que permiten modelar fenómenos de
contexto.
Cálculo Integral requiere como competencia previa todos los temas de Cálculo Diferencial
y a su vez proporciona las bases para el desarrollo de las competencias del Cálculo
Vectorial y Ecuaciones Diferenciales y asignaturas de física y ciencias de la ingeniería, por
lo que se pueden diseñar proyectos integradores con cualquiera de ellas.
La característica más sobresaliente de esta asignatura es que en ella se estudian las bases
sobre las que se construye el cálculo integral. Utilizando las definiciones de suma de
Riemann, integral definida para el cálculo de áreas. Para integral indefinida se consideran
los métodos de integración como parte fundamental del curso. La integral es tema de
trascendental importancia en las aplicaciones de la ingeniería.